Kombinasyon Hesaplama: Temel Bilgiler ve Uygulamalar
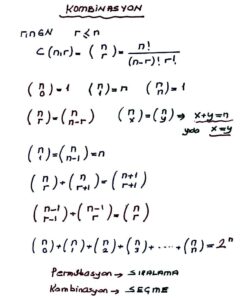 Kombinasyon, belirli bir nesne grubundan belirli sayıda nesne seçme işlemidir. Matematikte ve istatistikte sıkça karşılaşılan bu kavram, farklı durumları değerlendirmek ve olasılıkları hesaplamak için oldukça faydalıdır. Özellikle, kombinasyon hesaplama, öğrencilere birçok alanda yardımcı olabilecek bir beceridir. Bu yazıda, kombinasyonun ne olduğunu, nasıl hesaplandığını ve günlük hayattaki uygulamalarını öğreneceğiz.
Kombinasyon, belirli bir nesne grubundan belirli sayıda nesne seçme işlemidir. Matematikte ve istatistikte sıkça karşılaşılan bu kavram, farklı durumları değerlendirmek ve olasılıkları hesaplamak için oldukça faydalıdır. Özellikle, kombinasyon hesaplama, öğrencilere birçok alanda yardımcı olabilecek bir beceridir. Bu yazıda, kombinasyonun ne olduğunu, nasıl hesaplandığını ve günlük hayattaki uygulamalarını öğreneceğiz.
Kombinasyon Nedir?
Kombinasyon, belirli bir kümeden nesnelerin sırasız bir şekilde seçilmesini ifade eder. Örneğin, bir sınıfta 5 öğrenci varsa ve bu öğrencilerden 3'ünü seçmek istiyorsanız, bu kombinasyon hesaplama ile yapılır. Burada önemli olan nokta, seçtiğiniz nesnelerin sırasının önemi olmamasıdır. Yani A, B ve C seçimi ile B, C ve A seçimi aynı kombinasyonu oluşturur. Bu, kombinasyonun temel özelliklerinden biridir.
Kombinasyon Hesaplama Formülü
Kombinasyon hesaplamak için kullanılan formül şudur:
C(n, r) = n! / (r! * (n - r)!)
Burada:
- C(n, r): n elemanından r eleman seçilme kombinasyon sayısıdır.
- n!: n faktöriyel, yani n’in pozitif tam sayı olarak çarpımıdır.
- r!: r’nin faktöriyeli.
Sıkça Sorulan Sorular (SSS)
1. Kombinasyon ile Permütasyon arasındaki fark nedir?
Kombinasyon, nesnelerin sırasının önemli olmadığı durumları ifade ederken, permütasyon, nesnelerin sırasının önemli olduğu durumları ifade eder.
2. Kombinasyon hesaplaması neden önemlidir?
Kombinasyon hesaplaması, olasılık teorisi, istatistik ve günlük hayattaki birçok durum için karar verme süreçlerinde yardımcı olur.
3. Kombinasyon hesaplamak için bir formül var mı?
Evet, kombinasyon hesaplamak için genel formül: C(n, r) = n! / (r! * (n - r)!) şeklindedir.
4. Kombinasyon hesaplaması her durumda kullanılabilir mi?
Kombinasyon hesaplaması, nesnelerin sırasının önemli olmadığı durumlarda kullanılabilir. Sıralı durumlar için permütasyon kullanılır.
5. Kombinasyon hesaplaması yaparken dikkat edilmesi gerekenler nelerdir?
Kombinasyon hesaplaması yaparken, doğru faktöriyel hesaplamaları yapmak ve 'n' ile 'r' değerlerinin doğru bir şekilde belirlenmesi önemlidir.
